Corbel Design and Details

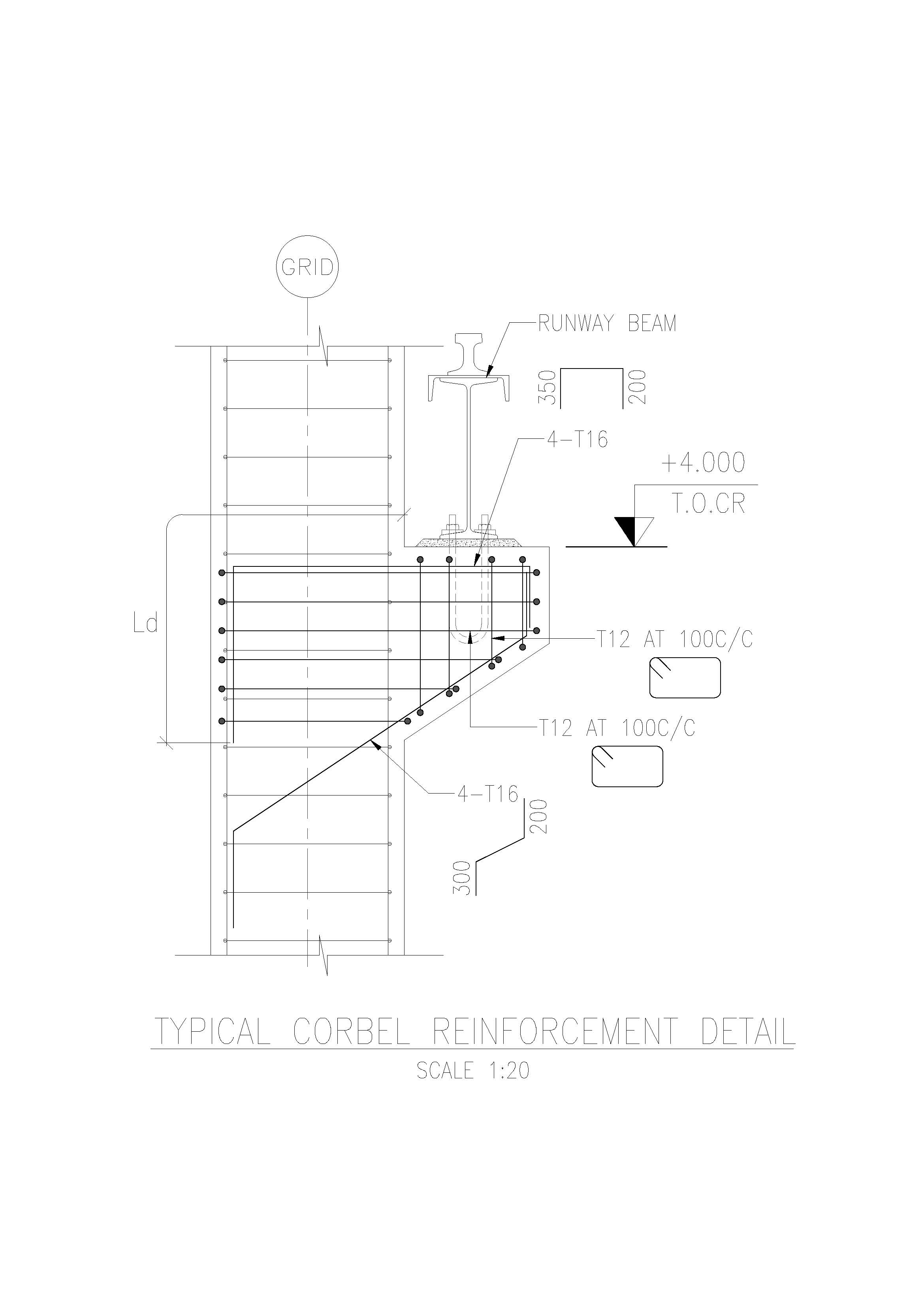
DESIGN OF CORBEL

A corbel is a short cantilever used to support structural loads like beams or girders projecting from a column or wall. It is commonly found in reinforced concrete and steel structures. The design of a corbel should ensure that it is capable of safely transferring vertical loads from beams to columns or walls.

Key Design Considerations for a Corbel:

Load Transfer Mechanism:
- Corbels are designed to transfer vertical loads, shear forces, and moments from beams or girders to columns or walls. The main forces acting on a corbel are shear and bearing stresses.
Dimensions:
- Depth (h): The depth of the corbel should be sufficient to resist shear and to avoid failure due to crushing. Typically, the corbel’s depth is about 0.5 to 0.7 times the depth of the supported beam.
- Projection Length (L): The projection should not exceed 1/2 of the effective depth (h) of the corbel to maintain stability and limit bending moments.
- Width (b): The width of the corbel is generally equal to the width of the supporting column or wall.
Reinforcement Design:
- Main Reinforcement: Reinforcing bars are provided near the top of the corbel to resist the tensile stresses. These bars should be anchored adequately into the column or wall.
- Shear Reinforcement: Shear links or stirrups are provided to resist vertical shear forces. Horizontal stirrups are also placed near the base of the corbel to handle diagonal tensile forces.
- Secondary Reinforcement: This includes anti-burst reinforcement, typically placed around the corbel to prevent bursting failure under concentrated loads.
Bearing Plate (if needed):
- A steel bearing plate may be used at the top of the corbel to distribute the load uniformly and prevent local crushing.
Anchorage:
- Proper anchorage of the reinforcement bars into the column or wall is critical to prevent failure. Hooks or bends in the reinforcement are provided to ensure proper load transfer.
Concrete Strength:
- High-strength concrete is typically used for corbels to resist high compressive stresses. A minimum grade of M25 or M30 concrete is common in such structures.

Design Procedure for a Corbel:

Determine Applied Loads:
- Vertical load PPP, and any horizontal load (if applicable).
Shear Stress Calculation:
- The shear force is given by V=PV = PV=P. The design should ensure the shear capacity of the concrete and reinforcement is adequate.
Check Bearing Stress:
- Ensure the bearing area between the corbel and the beam is large enough to prevent crushing of concrete.
Tension Reinforcement Design:
- Calculate the required area of steel based on the bending moment and tensile stresses. Reinforcing bars are placed in the top face of the corbel to resist the tensile force.
Shear Reinforcement Design:
- Determine the necessary shear reinforcement to resist vertical and horizontal forces.
Check for Failure Modes:
- Ensure the design addresses potential failure modes, including shear failure, crushing of concrete, and bursting failure.

Corbel Detailing:

Main Tension Reinforcement:
- These bars are placed near the top surface of the corbel and anchored into the column. They should extend beyond the theoretical cutoff point to prevent premature failure.
Shear Links:
- Vertical or horizontal stirrups are provided to resist shear and diagonal tensile forces. These links are placed along the height of the corbel.
Anti-Bursting Reinforcement:
- Additional reinforcement is provided near the base of the corbel to handle tensile stresses caused by the concentrated load acting on a small area.
Anchorage of Reinforcement:
- Reinforcement should be adequately anchored into the column, ensuring sufficient development length.

Typical Corbel Reinforcement Layout:

Main Reinforcement: Top layer with bars extending into the column.
Shear Stirrups: Vertical and horizontal shear links along the height of the corbel.
Additional Ties: Diagonal or horizontal reinforcement near the corbel’s bottom to resist bursting.

Corbel Design Example:

For a corbel supporting a vertical load PPP of 100 kN with a projection of 300 mm and a depth of 500 mm:

Determine the bending moment: M=P×LM = P \times LM=P×L, where LLL is the projection length.
Calculate required reinforcement based on the moment and the concrete’s tensile strength.
Check shear stress using appropriate shear reinforcement.
Ensure anchorage and bursting reinforcement are adequate for safe load transfer.

Corbel designs should adhere to the respective code provisions, such as IS 456:2000 for reinforced concrete design in India or ACI 318 in the U.S.

Data:

1 Wheel Load from the Crane = 10 T

2 Spacing of the Wheels = 3.15 m

3 Spacing of the Columns = 6 m

4 Width of Column = 450 mm

Consider the Load position shown below:

Taking Moments about B,

RA = 10 * (2.85 + 6) = 14.75 T

Take 15 T (considering Gantry Weight etc.)

Design Shear Force = 14.75 * 1.5 * 9.807 = 216.98 kN

Assuming an allowable stress in concrete as 1 Mpa the depth required = = 216.98 * 1000

1 * 450

= 483 mm

\ Overall depth required = 483 + 35 = 518 mm

Provide 600 mm over all depth

\ Effective Depth = 600 – 35 = 565 mm

Lever arm z = 0.85 * d = 0.85 * 565 = 480.25 mm

Moment at the Face of the Column = 216.98 * 0.35 = 75.943 kNm

As = M = 75.943 * 10^6

0.87 x z xfy 0.87 * 480.25 * 415

= 438 mm2

Ah = 0.5 As = 0.5 * 438 = 219 mm2

rv = As + Ah = 438 + 219 = 0.002584071

bd 450 * 565

Now, fc’ / fy = 0.8 * 25 / 415 = 0.049

\ 0.2 fc’ / fy = 0.2 * 0.049 = 0.0098

It is noted that 0.2 * fc’ / fy is < rv

Allowable Stress tv = 6.5 (1 – L / 2d) *(1 + 64rv)Ö fc’

= 281.5472836 psi

= 1.94 Mpa

Actual Shear Stress tv = 216.98 x 1000 = 0.854 Mpa 450 x 565

Allowable Stress tv > Actual Stress OK.

Note: The value of fc’ shall be in psi; In this case fc’ = 0.8 * 25 Mpa = 2899.4 psi

(Reference: Reinforce Concrete Structures by R. Park and T. Paulay, John Wiley and Sons)

Engineering Concepts

Corbel Design and Details

Categories

Recent Posts

Wind Load Calculation IS 875 Part 3 2015

Civil Structural Engineering Interview Questions pdf Free Download

Laboratory Building Plan and Architecture Details

Steel Shed with Mezzanine Floor

HOUSE PLAN 30 X 60 | SOUTH FACING |

Unit Converter – Feet, Inches, cm, mm, Yard to Meter and Vice Versa

Fencing Gate Details and Requirements

Thrust Blocks and Restraints Details

Civil Engineering Formula Book | Pocket Guide pdf Free download |

Steel Staircase Design