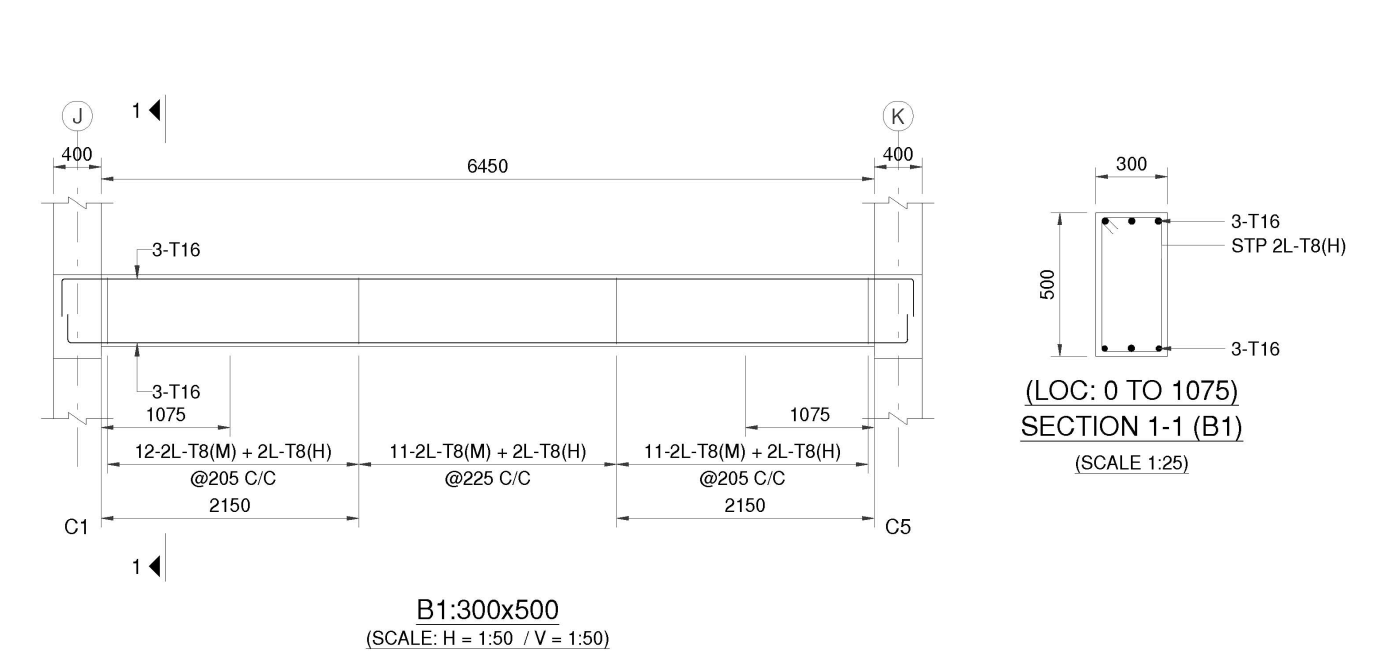
Concrete Beam Design as per Canadian Code (CSA A23.3-19)

The design of concrete beams in Canada is governed by CSA A23.3-19: Design of Concrete Structures, which provides guidelines for strength, serviceability, and durability of reinforced concrete elements. Below is a step-by-step approach to designing a concrete beam according to the Canadian code.

1. Key Parameters for Beam Design

Material Properties:

• Concrete Strength (f′c):
  • Typically ranges from 20 MPa to 50 MPa.
• Reinforcement Steel (fy​):
  • Yield strength: 400 MPa or 500 MPa (common for rebar in Canada).

Load Considerations:

• Factored Loads:
  • Factored dead load (D_f ​) and factored live load (L_f​).
  • Load combinations as per CSA A23.3-19 Clause 8.1:
    • 1.25D + 1.5L (for beams).
• Self-weight:
  • Concrete density: 24 kN/m³

2. Assumptions for Flexural Design

Cross-Sectional Properties:

• Rectangular beam: width (b), effective depth (d).
• Neutral axis depth (c): determined iteratively during the design.

Assumptions:

• The concrete in tension is neglected.
• Steel reinforcement resists all tensile forces.
• Compression is resisted by concrete in the compression zone.

3. Flexural Strength Design

Step 1: Nominal Moment Capacity (Mn​)

The nominal moment capacity for a singly reinforced beam is given by:

Mn= ϕ ⋅ As ⋅ fy ⋅ (d−a/2)

Where:

• As ​: Area of tensile reinforcement (As = n ⋅ π ⋅ d_b²/4).
• a : Depth of equivalent rectangular stress block (a = β1 ⋅c ).
• β1: Factor based on f′c (from CSA Table 10.2.1).

Step 2: Solve for Reinforcement Area (As​)

For a given factored moment (Mu​):

As = Mu ϕ ⋅ fy ⋅ (d−a/2)

Where:

• ϕ : Resistance factor (typically 0.85 for flexural design).
• Mu ​: Factored bending moment.

4. Shear Design

Shear Strength (Vc and Vs​)

The shear resistance (Vr​) is the sum of contributions from concrete (Vc​) and stirrups (Vs​):

Vr = ϕ ⋅ (Vc + Vs)

Concrete Contribution (Vc ):

Vc = 0.166 ⋅ f′c ⋅ b ⋅ d

1. Stirrups Contribution (Vs​):

Vs = Av ⋅ fy ⋅ ds ​

Where:

• Av : Area of stirrups.
• S: Stirrup spacing.

5. Serviceability Checks

Deflection Control:

• Ensure span-to-depth ratio satisfies serviceability requirements.
• CSA provides limits based on beam type and loading.

Crack Control:

• Reinforcement spacing must ensure crack widths are within acceptable limits.

6. Durability Considerations

Minimum Reinforcement:

• Provide minimum reinforcement to prevent sudden failure:

As ≥ 0.2 ⋅ b ⋅ d/fy

Clear Cover:

• Ensure adequate concrete cover for durability:
  • 25 mm: Interior beams.
  • 40 mm : Exterior beams.

Example: Design a Rectangular Beam

Given Data:

• Factored moment (Mu ​): 150 kNm
• Beam dimensions: b=300 mm,d=500 mm
• f′c=30 Mpa, fy=400 Mpa

Step 1: Calculate a

β1=0.85 (from CSA Table 10.2.1 for f′c=30)

Assume a ≈ 0.1d =50 mm

Step 2: Calculate As

Substitute values into the moment formula:

As= Mu

Φ ⋅ fy ⋅ (d−a/2)

​​ As = 150,0000

0.85 ⋅ 400 ⋅ (500−25) ≈ 880 mm2

Provide 3 ϕ16 mm3

Step 3: Check Shear

Use Vc​ and Vs​ formulas for shear design and ensure Vr≥Vu

This process ensures the beam complies with CSA A23.3-19 for strength, serviceability, and durability. Here’s a detailed guide and example for the design of a rectangular concrete beam as per CSA A23.3-19 standards:

Step-by-Step Concrete Beam Design Process

1. Problem Statement:

Design a simply supported concrete beam to resist the following loads:

• Span (L): 6 meters
• Factored loads:
  • Dead load (Df​): 10 kN/m
  • Live load (Lf​): 15 kN/m
• Material properties:
  • Concrete compressive strength (fc′​): 30 MPa
  • Steel yield strength (fy​): 400 MPa

2. Preliminary Section Dimensions

Choose approximate dimensions for the beam based on the span-to-depth ratio:

Effective Depth (d)= Span

16 to 20

Assume b=300 mm, d=500 mm

3. Flexural Design

Step 1: Factored Moment (Mu​)

1. Total factored load per unit length (wu​):

Wu = 1.25Df + 1.5Lf = 1.25(10) + 1.5(15)=31.25 kN/m

Maximum factored moment (Mu​) for a simply supported beam:

Mu = wuL² / 8 = 31.25⋅628 = 140.63 kNm

Step 2: Calculate Depth of Stress Block (a)

Using the stress block formula:

a=β1​c

Where:

• β = 0.85
• c : Distance from the extreme compression fiber to the neutral axis.

Step 3: Reinforcement Area (As​)

The nominal moment capacity is given by:

Mn = As . fy (d−a/2)

Rearrange to solve for As​:

As=Mu / ϕ.fy. (d − a/2)

Substitute:

• ϕ=0.85 (resistance factor for flexure)
• Assume a=50 mm

As= 140.63 ⋅ 10⁶

0.85 ⋅ 400 ⋅ (500−25) ≈880.75 mm2

Provide 3 bars of 16 mm diameter reinforcement:

As= 3⋅ π / 4 ⋅ (16)2=904.78 mm2

This satisfies the required As

4. Shear Design

Step 1: Factored Shear Force (Vu​)

The maximum shear force at the support is:

Vu = wu . L/ 2 =(31.25 ⋅ 6 / 2) = 93.75 kNV_

Step 2: Shear Resistance (Vr​)

The total shear resistance is:

Vr = ϕ ⋅ (Vc+Vs)

1. Concrete Contribution (Vc​):

Vc = 0.166 ⋅ fc′ . b ⋅ d

Vc = 0.166 ⋅ 30 ⋅ 300 ⋅ 500 = 216.1 KN

1. Steel Contribution (Vs​): If additional reinforcement is needed:

Vs = Av ⋅ fy ⋅ ds

Where:

• Av ​: Area of stirrup legs (e.g., 2 ⋅π ⋅10²/4 =157 mm2,
• s: Stirrup spacing.

Assume s=200 mms:

Vs=157 ⋅ 400⋅ 500 / 200 ⋅ 1000 = 157 kN/m

5. Deflection Check

For serviceability:

• Check span-to-depth ratio against allowable limits from CSA Table 9.1.

6. Durability and Cover

• Provide clear cover as per CSA standards:
  • 25 mm for interior beams.
  • 40 mm for exterior beams.
• Ensure crack control by limiting spacing of tensile steel bars to:

Max spacing=300 mm or less

Summary

• Beam Size: b=300 mm, d=500 mm
• Reinforcement:
  • Flexure: 3 ϕ16 mm bars.
  • Shear: Stirrups of 2 ϕ10 mm spaced at 200mm.
• Shear Resistance:
  • Vc=216.1 kN, Vr=373.1 kN

This ensures the beam satisfies flexural strength, shear resistance, and serviceability as per CSA A23.3-19.

• 3D HOUSE DESIGN (9)
• Civil and Structural Design Calculations (31)
• Commercial Plans (5)
• Engineering Concepts – Civil & Structural (88)
• Excel Spreadsheets (16)
• House Plans (38)
• Industrial standards (28)