DESIGN OF SLABS AS PER IS456
1. GENERAL
A slab is a flat two dimensional planar structural element having thickness small compared to its other two dimensions. It provides a working flat surface or a covering shelter in buildings. It primarily transfers the load by bending in one or two directions. Reinforced concrete slabs are used in floors, roofs and walls of buildings and as the decks of bridges. The floor system of a structure can take many forms such as in situ solid slab, ribbed slab or pre-cast units. Slabs may be supported on monolithic concrete beam, steel beams, walls or directly over the columns. Concrete slab behave primarily as flexural members and the design is similar to that of beams.
The design of slabs involves determining their thickness, reinforcement, and strength to resist loads safely. The classification into one-way and two-way slabs is based on the aspect ratio (Ly/Lx) of the slab panel, where Ly is the longer span and Lx is the shorter span.
One-Way Slab:
Slab supported on two opposite sides.
Load is primarily carried along the shorter span (Lx).
Condition: Ly / Lx ≥ 2.
Two-Way Slab:
Slab supported on all four sides.
Load is carried in both directions.
Condition: Ly / Lx < 2.
2. CLASSIFICATION OF SLABS
Slabs are classified based on many aspects
- Based of shape: Square, rectangular, circular and polygonal in shape.
- Based on type of support: Slab supported on walls, Slab supported on beams, Slab supported on columns (Flat slabs).
- Based on support or boundary condition: Simply supported, Cantilever slab, Overhanging slab, Fixed or Continues slab.
- Based on use: Roof slab, Floor slab, Foundation slab, Water tank slab.
- Basis of cross section or sectional configuration: Ribbed slab /Grid slab, Solid slab, Filler slab, Folded plate
6) Basis of spanning directions :
One way slab – Spanning in one direction Two way slab _ Spanning in two direction
In general, rectangular one way and two way slabs are very common and are discussed in detail.
3. METHODS OF ANALYSIS
The analysis of slabs is extremely complicated because of the influence of number of factors stated above. Thus the exact (close form) solutions are not easily available. The various methods are:
- Classical methods – Levy and Naviers solutions(Plate analysis)
- Yield line analysis – Used for ultimate /limit analysis
- Numerical techniques – Finite element and Finite difference method.
- Semi empirical – Prescribed by codes for practical design which uses coefficients.
4. GENERAL GUIDELINES
a. Effective span of slab :
Effective span of slab shall be lesser of the two
- l = clear span + d (effective depth )
- l = Center to center distance between the support
b. Depth of slab:
The depth of slab depends on bending moment and deflection criterion. the trail depth can be obtained using:
- Effective depth d= Span /((l/d)Basic x modification factor)
- For obtaining modification factor, the percentage of steel for slab can be assumed from 0.2 to 0.5%
- The effective depth d of two way slabs can also be assumed using cl.24.1,IS 456 provided short span is ≤ 3.5m and loading class is < 3.5KN/m2
| Type of support | Fe-250 | Fe-415 |
| Simply supported | l/35 | l/28 |
| continuous | l/40 | l/32 |
OR
The following thumb rules can be used
- One way slab d=(l/22) to (l/28).
- Two way simply supported slab d=(l/20) to (l/30)
- Two way restrained slab d=(l/30) to (l/32)
c. Load on slab:
The load on slab comprises of Dead load, floor finish and live load. The loads are calculated per unit area (load/m2).
Dead load = D x 25 kN/m2 ( Where D is thickness of slab in m) Floor finish (Assumed as)= 1 to 2 kN/m2
Live load (Assumed as) = 3 to 5 kN/m2 (depending on the occupancy of the building)
5. DETAILING REQUIREMENTS AS PER IS 456 : 2000
a. Nominal Cover :
For Mild exposure – 20 mm
For Moderate exposure – 30 mm
However, if the diameter of bar do not exceed 12 mm, or cover may be reduced by 5 mm. Thus for main reinforcement up to 12 mm diameter bar and for mild exposure, the nominal cover is 15 mm
- Minimum reinforcement : The reinforcement in either direction in slab shall not be less than
- 0.15% of the total cross sectional area for Fe-250 steel
- 0.12% of the total cross sectional area for Fe-415 & Fe-500 steel.
- Spacing of bars : The maximum spacing of bars shall not exceed
- Main Steel – 3d or 300 mm whichever is smaller
- Distribution steel –5d or 450 mm whichever is smaller Where, ‘d’ is the effective depth of slab.
Note: The minimum clear spacing of bars is not kept less than 75 mm (Preferably 100 mm) though code do not recommend any value.
- Maximum diameter of bar: The maximum diameter of bar in slab, shall not exceed D/8, where D is the total thickness of slab.
6. BEHAVIOR OF ONE WAY SLAB
When a slab is supported only on two parallel apposite edges, it spans only in the direction perpendicular to two supporting edges. Such a slab is called one way slab. Also, if the slab is supported on all four edges and the ratio of longer span(ly) to shorter span (lx) i.e ly/lx > 2, practically the slab spans across the shorter span. Such a slabs are also designed as one way slabs. In this case, the main reinforcement is provided along the spanning direction to resist one way bending.

Fig.1: Behavior of one way slab
7. BEHAVIOR OF TWO WAY SLABS
A rectangular slab supported on four edge supports, which bends in two orthogonal directions and deflects in the form of dish or a saucer is called two way slabs. For a two way slab the ratio of ly/lx shall be ≤ 2.0 .

Fig. 2: Behavior of Two way slab
Since, the slab rest freely on all sides, due to transverse load the corners tend to curl up and lift up. The slab looses the contact over some region. This is known as lifting of corner. These slabs are called two way simply supported slabs. If the slabs are cast monolithic with the beams, the corners of the slab are restrained from lifting. These slabs are called restrained slabs. At corner, the rotation occurs in both the direction and causes the corners to lift. If the corners of slab are restrained from lifting, downward reaction results at corner & the end strips gets restrained against rotation. However, when the ends are restrained and the rotation of central strip still occurs and causing rotation at corner (slab is acting as unit) the end strip is subjected to torsion.
7.1 Types of Two Way Slab
Two way slabs are classified into two types based on the support conditions:
- Simply supported slab
- Restrained slabs
7.1.1 Two way simply supported slabs
The bending moments Mx and My for a rectangular slabs simply supported on all four edges with corners free to lift or the slabs do not having adequate provisions to prevent lifting of corners are obtained using
Mx = αx W l2x My = αy W l2x
Where, αx and αy are coefficients given in Table 1 (Table 27,IS 456-2000)
W- Total load /unit area
lx & ly – lengths of shorter and longer span.
Table 1 Bending Moment Coefficients for Slabs Spanning in Two Directions at Right Angles, Simply Supported on Four Sides (Table 27:IS 456-2000)
| ly/lx | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.75 | 2.0 | 2.5 | 3.0 |
| αx | 0.062 | 0.074 | 0.084 | 0.093 | 0.099 | 0.104 | 0.113 | 0.118 | 0.122 | 0.124 |
| αy | 0.062 | 0.061 | 0.059 | 0.055 | 0.05 1 | 0.046 | 0.037 | 0.029 | 0.020 | 0.014 |
Note: 50% of the tension steel provided at mid span can be curtailed at 0.1lx or 0.1ly from support.
7.1.2 Two way Restrained slabs
When the two way slabs are supported on beam or when the corners of the slabs are prevented from lifting the bending moment coefficients are obtained from Table 2 (Table 26, IS456-2000) depending on the type of panel shown in Fig. 3. These coefficients are obtained using yield line
theory. Since, the slabs are restrained; negative moment arises near the supports. The bending moments are obtained using;
Mx (Negative)= αx (-) W l2x
Mx (Positive)= αx (+) W l2
My (Negative)= αy (-) W l2x
My (Positive)= αy (+) W l2

Fig. 3: Different Boundary conditions of Two way Restrained slabs
Table 2: Bending moment coefficients for two way restrained slabs ( Table 26, IS 456-2000)
Detailing requirements as per IS 456-2000
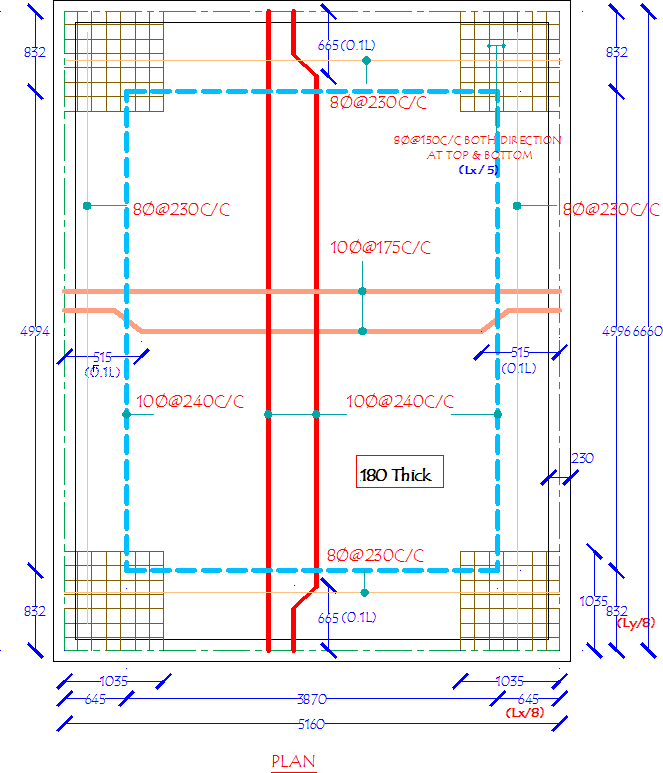
- Slabs are considered as divided in each direction into middle and end strips as shown below
- The maximum moments obtained using equations are apply only to middle strip.
- 50% of the tension reinforcement provided at midspan in the middle strip shall extend in the lower part of the slab to within 0.25l of a continuous edge or 0.15l of a discontinuous edge and the remaining 50% shall extend into support.
- 50% of tension reinforcement at top of a continuous edge shall be extended for a distance of 0.15l on each side from the support and atleast 50% shall be provided for a distance of 0.3l on each face from the support.

- At discontinuous edge, negative moment may arise, in general 50% of mid span steel shall be extended into the span for a distance of 0.1l at top.
- Minimum steel can be provided in the edge strip
- Tension steel shall be provided at corner in the form of grid (in two directions) at top and bottom of slab where the slab is discontinuous at both the edges . This area of steel in each layer in each direction shall be equal to ¾ the area required (Ast) for maximum mid span moment. This steel shall extend from the edges for a distance of lx/5. The area of steel shall be reduced to half (3/8 Astx) at corners containing edges over only one edge is continuous and other is discontinuous.
Fig. 4: Reinforcement details and strips in Two way restrained slabs

8. ONE WAY CONTINUOUS SLAB
The slabs spanning in one direction and continuous over supports are called one way continuous slabs.These are idealised as continuous beam of unit width. For slabs of uniform section which support substantially UDL over three or more spans which do not differ by more than 15% of the longest, the B.M and S.F are obtained using the coefficients available in Table 12 and Table 13 of IS 456-2000. For moments at supports where two unequal spans meet or in case where the slabs are not equally loaded, the average of the two values for the negative moments at supports may be taken. Alternatively, the moments may be obtained by moment distribution or any other methods.
Table 3: Bending moment and Shear force coefficients for continuous slabs ( Table 12, Table 13, IS 456-200)


DESIGN EXAMPLES